|
|
|
|
|
| |
There is a family of strategies which rely on Sudoku puzzles having one single solution. This is very much the norm with all published Sudokus since no puzzle compiler would want to annoy their audience with puzzles that have two or more solutions. It’s easy to create a sudoku with more than one solution simply by missing of a clue or changing one. If it doesn’t lead to an error it will more often that not lead to non-uniqueness.
The following three strategies – Unique Rectangles, Empty Rectangles and the wonderfully named Bi-value Universal Grave (BUG) all rely on unique solutions to work. If that proviso is admitted then pure logic let’s us do some fancy footwork. |
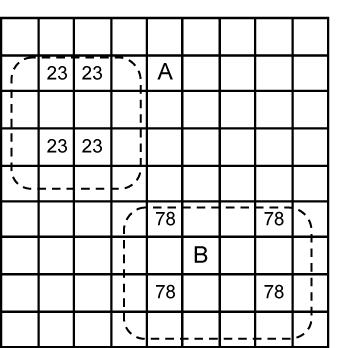
Fig. 24.1 |
In this diagram we have two rectangles formed from four cells apiece. There is a crucial difference between both of them; one of these is a “Deadly Pattern” and the other is a valid spread of candidates. Both contain four sets of pairs or bi-value cells.
The set with 2/3’s in box A is spread over two rows, two columns and two boxes
|
|
Such a group of four pairs is impossible in a Sudoku with one solution. The reason? Pick any cell with 2/3. If the cell solution was 2 then we quickly know what the other three cells are. But it would be equally possible to have 3 in that cell and the others would be the reverse. There are two solutions to any Sudoku with this deadly pattern. If you have achieved this state in your solution something has gone wrong.
The pattern marked B looks like a deadly pattern but there is a crucial difference. The 7/8 still resides on two rows and two columns, but instead if two boxes it is spread over four boxes. Now, such a situation is fine since you can't guarantee that swapping the 7 and 8 in an alternate manner will produce two valid Sudokus. One of them is the real solution, the other a mess. Why? Swapping the 7 and 8 around places them in different boxes and 1 to 9 must exist in each box only once. In example A, swapping within the box does not change the content of that box.
For all Unique Rectangles we are going to look for potential deadly patterns and take advantage of them. This means one of the corners could become a deadly pattern if certain candidates were removed. Above all, we don’t want to create a Deadly Pattern and because the Sudoku is assumed to have one solution we can take advantage of this knowledge to crack it. |

Fig. 24.2
|
A Type 1 Unique Rectangle is illustrated above. The three circles contain 3/9. The fourth corner marked in a dark shape also contains 3/9 and one other candidate, a 4. If the 4 were removed from that cell we would have a Deadly Pattern. This cannot be allowed to happen so it’s safe to remove 3 and 9 from that cell.
Once the logic is mastered the proof is fairly straightforward. Assume H6 is 3. That forces H4 to be 9, D6 to be 9 as well, and D4 to be 3. That's the deadly pattern; you can swap the 3's and 9's and the puzzle still can be filled in. So if the Sudoku is valid, H6 cannot be 3. The exact same logic applies if you assume H6 is 9.
So H6 can't be a 3, and can't be a 9 - it must be either 4. This works because the four cells are in two rows, two columns and just two boxes. |
|
Below we have a similar pattern, but this time, B4 and B6 (shaded cells at the top), the squares which share the same block have a single extra possibility - in this case, 8. |
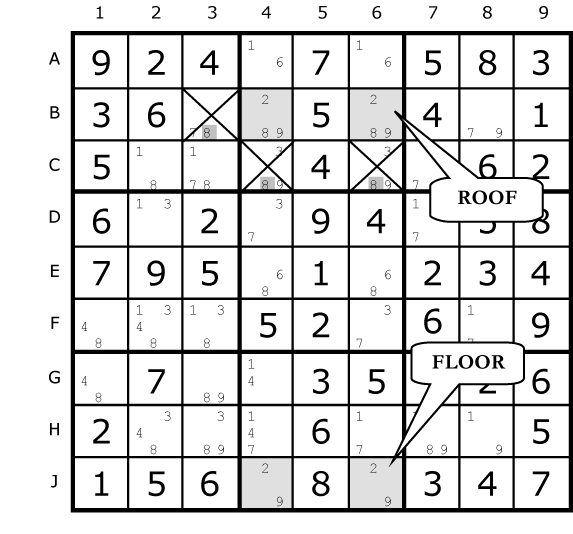
Fig. 24.3
|
The convention when talking about the four cells in this Unique Rectangle is to use the term “Floor cells” to refer to bi-value cells and the “Roof cells” for the ones with extra candidates (2/8/9 in this case). The Floor cells are our foundation for the rectangle and the roof is the active part. But it’s certainly possible for them to be upside down.
In Type-2, one of the boxes contains the floor squares, and the other contains the roof squares. In order to avoid the deadly pattern, 8 must appear in either B4 or B6 (the roof squares). Therefore, it can be removed from all other squares in the units (row, column and box) that contain both of the roof squares (in this case, row B and box 2).
Now that we've gotten our heads around the basic unique rectangle concept, the proof should be clear: If neither B4 nor B6 contains an 8, then they both become squares with possibilities 2/9. This results in the deadly pattern - so one of those squares must be the 8, and none of the other squares in the intersecting groups can contain the 8. So B3, C4 and C6 can have 8 removed. |
The Type 2 marked here, once completed, reveals a second one.
Can you find it? |
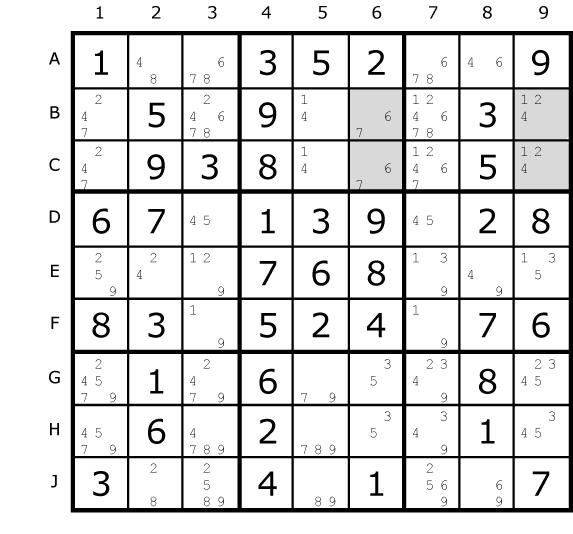
Fig. 24.4 |
|
There is a second variant of Type-2 Unique Rectangles as illustrated below.
In this puzzle, we have the same pattern of 4 squares in 2 blocks, 2 rows and 2 columns. The floor squares are A1 and A9, and the roof squares are B1 and B9. However, in this Unique Rectangle, each of the blocks contains one floor and one roof square. This is perfectly fine, but it means that the only unit (row/column/box) that contains both of the roof squares is row 2, so that is the only unit that you can attempt to reduce; in this case, B7 cannot contain a 8. |
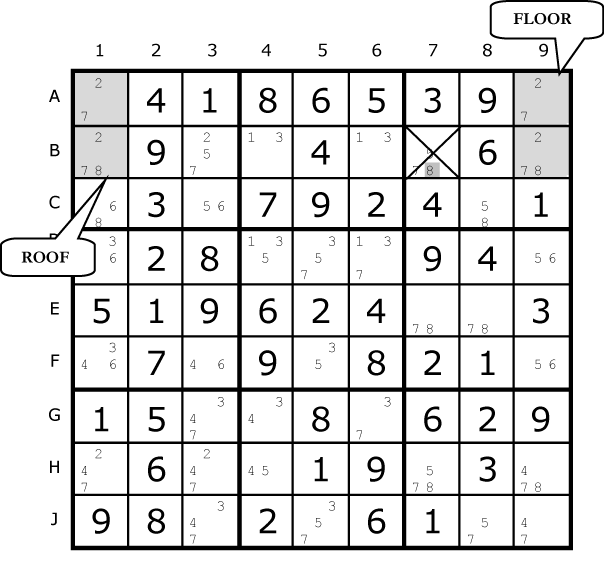
Fig. 24.5
|
|
Type 4 concerns actually removing one or more candidates from the roof.
Let’s have a close look at this example: |

Fig. 24.6
|
The roof cells are C1 and C3 because they contain the extra candidate 6. Without 6 a deadly pattern would form. But let’s leave 6 alone and look at the 1/5 in the roof. The peculiar characteristic is that in box 1, the roof squares are the only squares that can contain a 5. This means that, no matter what, one of those squares must be 5. Say C1 contained the 5, 1 is exclude from C3 since it would form the deadly pattern. The same would be true if C1 were 5. Since these are the only alternatives, we can conclude that neither of the cells can contain a 1. So we can remove 1 from C1 and C3.
This is an example of a "Type-4 Unique Rectangle". As you have probably realized, since the roof squares are in the same block, you can search for conjugate pairs in both of their common units (the row and the block, in this case). |
|
By now you’ll recognise that there is a B variant for each Unique Rectangle (Type 1 contains both variants within itself since the extra candidate exists only in one corner).
In a Type-4B Unique Rectangle variant the floor squares are not in the same block, and you can only look for the conjugate pair in their common row or column. For example: |

Fig. 24.7
|
In this case, since 7 can only appear in row D in the roof squares, 5 can be removed from both D5 ad D7.
As Type-4 Unique Rectangle solutions "destroy" the Unique Rectangle, it is usually best to look for them only after you've done any other possible Unique Rectangle reductions. |
| |