|
|
|
|
|
This is a clever but obscure spin on uniqueness in a Sudoku. An Empty Rectangle occurs within a box where four cells form a rectangle and do NOT contain a certain candidate.
In Figure 1 we have some example spreads of candidate 8 within several boxes. For this work there must be more than two candidates in a box and four or more cells “empty” cells. |
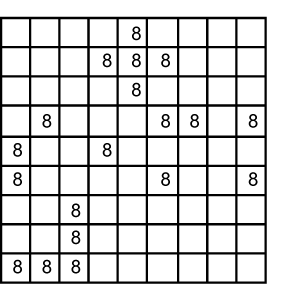
Fig. 25.1 |
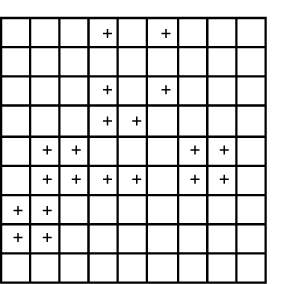
Fig. 25.2 |
|
In Figure 25.2 we can draw the Empty Rectangles (ERs); the corners are marked by plus signs. Each of these theoretical rectangles is independent of each other since the trick occurs within a box. |

Fig. 25.3 |
Whatever the formation of the ER you will have a gap vertically and horizontally where we can imagine two Empty Rectangle Lines (ERLs). These are two lines we can draw inside the box without touching the ER itself. |
|
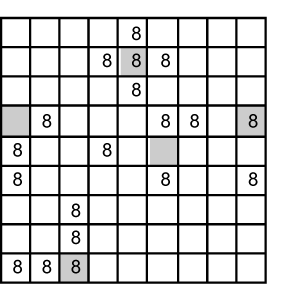
Fig. 25.4 |
These lines we can quickly forget once we’ve spotted where they cross – known as the Empty Rectangle Intersection (ERI).
For the examples the ERI has been marked in a dark shaded cell. |
|
| And how is this useful? A strong link connects two cells where a candidate occurs only twice in that unit. If you have a strong link and an ERI that shares a line (row or column) then you can eliminate a candidate at the point where the other end of the strong link and the ERI intersect. Before we prove how this works, some visual examples of the formation: |
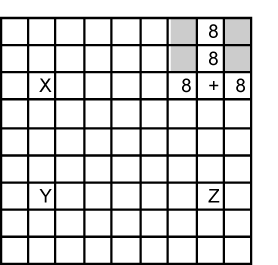
Fig. 25.5.1 |
The plus sign now indicates where the Empty Rectangle Intersection (ERI) is placed. In column 2 two 8’s exist and form strong link (X and Y). One end of the strong link (X at C2) can see the ERI at C8.
The ERI and the other end of the strong link (Y at H2) can see Z at H8. If a candidate 8 exists there it can be removed.
|

Fig. 25.5.2 |

Fig. 25.5.3 |
| |
|
|
| Here is a real life example based on number 6. Our Empty Rectangle is shaded dark in box 4. The Empty Rectangle Intersection is E1 marked by a dashed hexagon. We have a strong link on 6 between E7 and H7. H1 is the intersection between the ERI and the far end of the strong link. The 6 in H1 can be removed and the Sudoku solved. |
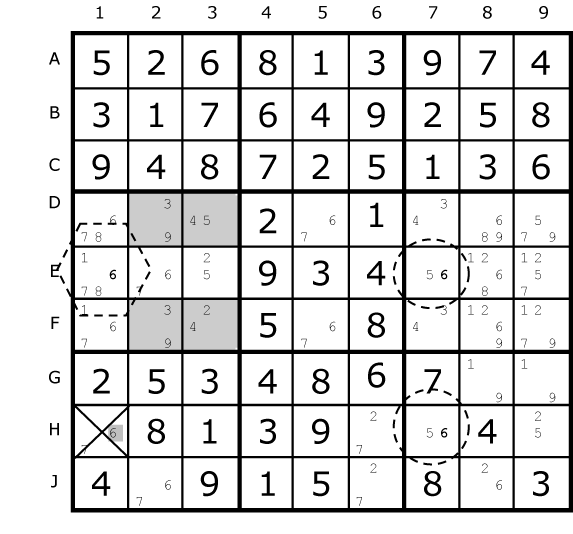
Fig. 25.6 |
To show how Empty Rectangles work we need to consider the dual options for the strong link. One end or the other is going to be true, that is in the example above, 6 will occur either at E7 or H7. If the solution is H7 then 6 cannot be at H1. This is the easy half of the proof. Now we have to check what happens if E7 is 6 and show this leads to the removal of 6 at H1.
Our ERI cell is aligned with both the X in our strong link and the target cell Z. This means that all our candidates spread within box are either aligned with X in our strong link or with the target cell Z. |

Fig. 25.7 |
In our real life example we pretend to set X to true (marked T) and Y to false (marked F). We mentally eliminate other 6’s from row E.
What we are left with are 6’s in column 1. These form a hidden pair and therefore a 6 elsewhere in the column is impossible. Ergo, we have proved Z cannot contain a 6.
|
|
There is a second Empty Rectangle in this example which is also based on number 6 and is simultaneous with the first |

Fig. 25.8 |
| The ERI at E8 points to a target cell at J8. We have a strong link in column 2 at E2 and H2. The same logic applies and it’s safe to remove the 6 at J8. |