|
|
|
|
|
This is an excellent candidate eliminator (and is also known as XY-Wing). The name derives from the fact that it looks like an X-Wing - but with three corners, not four. The forth corner is where the candidate can be removed but it leads us to much more as we'll see in a minute.
Let’s look at Figure 19.1 for the theory. |
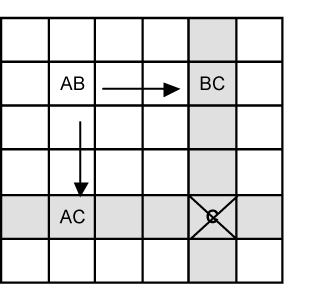
Fig. 19.1 |
A is a conjugate pair and so is B. That is the candidate number represented by A only exists twice in the column. B also only exists twice in its row.
AB is a bi-value cell (it only has two candidates). The bottom left cell marked AC is also bi-value and so is BC. C is the common candidate between AC and BC.
Fine and dandy. |
|
The cell marked AB is the ‘hinge’. If the solution to that cell turns out to be A then C will definitely occur in the lower left corner. If AB turns out to be B then C is certain to occur in the top right. AC/BC is a complimentary pair, meaning they will both be either true or false.
So whatever happens, C is certain in one of those two cells marked AC or BC. The cell marked with a cross can be 'seen' by both Cs - the cell is a confluence of both BC and AC. It’s impossible for a C to live there and if C resides there it can be evicted. |
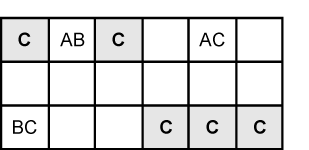
Fig. 19.2 |
If our A, B and C are aligned more closely they can 'see' a great deal more cells than just the corner of the rectangle they make. In Figure 2 B is a locked pair because they share the same box. A is a locked pair because they share the same row. BC and AC can see all the cells marked with a C where elimination can occur. |
|

Fig. 19.3
|
| |
Here is a classic Y-Wing beginning with the hinge at C4. If C4 is a 6 then C1 must be a 4. Otherwise if C4 is an 8 then G4 is a 4. Either way the far corner at G1 can’t be a 4. |
|
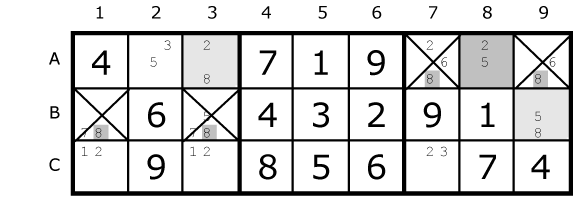
Fig. 19.4
|
This example starting with the hinge at A8 removes four 8’s from the first two rows. This is because the alignment between A3 and B9 means they both see six common cells. |