|
|
|
|
|
Now we’ve seen how chains are formed and can be applied we can take the idea to the next level. This is where more than one chain is present on the board. We’ve still considering only one number at a time (which is a relief) but often the pairs that form create several disconnected chains. Remember, a link in a chain can only be formed if exactly two occurrences of a number exist in a unit so three or more will ‘block’ a chain from continuing. |
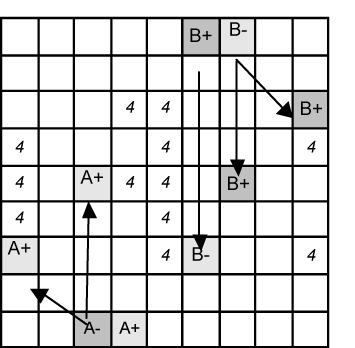
Fig. 18.1 |
Here we have two sets of chains on the number 4. For clarity all numbers have been removed except the 4 candidates. Where 4’s are part of a chain they have been overtyped with A+/A- and B+/B- to show the pairs and the links in the chains.
We can’t connect the chains since there are other 4’s in the way. |
|
Given two chains we can label them A and B. A+ and A- will indicate the alternating states so that EITHER all of A+ are true OR all of A- are true. We don't know which way round yet. Similarly B+ and B- indicate alternating true/false for that chain. C+ and C- continues the theme if there are more chains on the same candidate number. Given A+, A-, B+ and B- we can colour them on the board to see the patterns.
Let’s look at the multi-colouring rules.
Type 1 Multi-Colouring
The Rule is as follows: If A+ shares a unit with B+ and B- then A+ must be the false candidate since either B+ or B- must be true.
We can see above that E3(A+) can see E7(B+)
and G1(A+) can see G6(B-). None of the A+ cells can be 4.
This second example illustrates the idea further, based on candidate 9. The B chain is a single pair. |
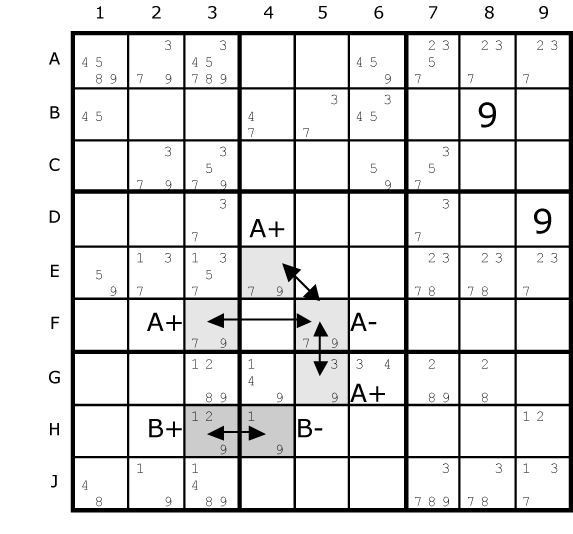
Fig. 18.2 |
A+ is again the victim and all the labels are the same as the first example.
It also shows that the chains can be quite short. All three cells marked A+ must have their 9’s removed.
Interestingly, although B can be a chain of just two cells A must be a longer chain. Otherwise we'd be in a situation where the sudoku has two solutions or multi-colouring can be reduced to a Unique Rectangle, discussed later.
Type 2 Multi-Colouring
If A+ shares a unit with B+ then any cell with the given candidate and sharing a unit with both A- and B- can have that candidate excluded. The Reason: Since A+ and B+ can't both be true, then either one or both of A- and B- must be true. Therefore any cell sharing a unit with both A- and B- can safely have that candidate excluded.
This is a bit of a mouthful. What we're looking at are cells marked A+ which can see B+ cells but A- cells cannot see B- cells. A+ and B+ both can't be true since they share units two cases. One or perhaps both of the groups marked A- and B- must be true. |
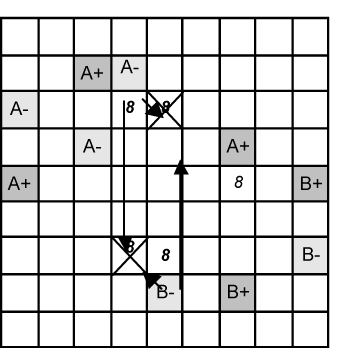
Fig. 18.3 |
All cells that can see an A- and a B- can't contain the candidate, in this example number 8. In C5 an 8 can see B4 and H5. Similarly the 8 in G4 can see B4 and G9/H5. |
| |
This smaller example might be easier to understand. The labels are the same so that one A+ can see a B+ (dashed line).
There is just one place where a 7 is at the overlap of an A- and a B-. |
|
| |
There is a lesson here that there is often more than one way to skin a cat.
We can re-formulate the X-Wing strategy in terms of Type 2 multi-colouring.
X-Wing is far simpler but we can show it is a special case of this strategy. |
|
Let us take the example found earlier in the book and show that the two pairs of 6 in rows B and H are actually very short chains. To eliminate other 6’s in column 5 we must label the X-Wing cells as above. Now, A+ and B+ can see each other so they “share a unit” so any candidate 6 “sharing a unit with both A- and B- can have that candidate excluded” which are all others 6’s in column 5. To get the 6’s in column 2 we have to reverse the A+/- and B+/-.
Multi-colouring also applies to Sword-Fish and Jelly-Fish. |
|

Fig. 18.6 |
All the cells containing 2 have been highlighted. Study the distribution of 2’s and find the strong and weak links. (Strong being only two 2’s in a unit). You should find two chains. They can be compared and the Type 2 rule will apply. One 2 not in either chain can be eliminated because it can be see by both chains. You’ll have to mark which cells are A+,B+,A- and B-. Answer on page X. |