|
|
|
|
|
However, we’re not at the end of the story as far as this strategy goes. We should also be looking to remove candidates within a box because of a row or column. This is sometimes called Box/Line Reduction but is really just a type of Intersection Removal. Let’s look at this central strip of a Sudoku |
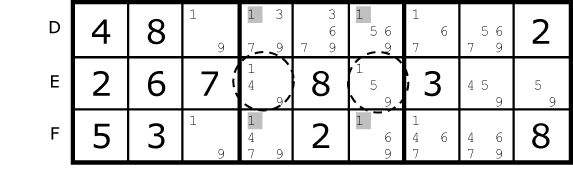
Fig. 11.1 |
The 1’s in row E are the only two 1’s on that row. They both exist in the same box. The row intersections box 5. Because a 1 must appear on that row we can remove the 1’s from the rest of the box. We get four in this case. There is no problem tripling this strategy up: |
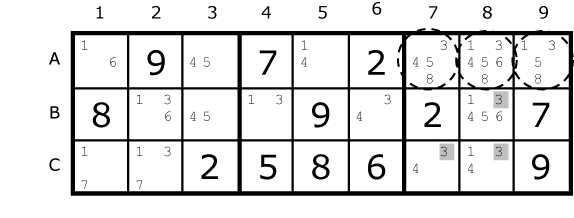
Fig. 11.2 |
Here there are three 3’s in the top row which means we can remove them from the rest of box 3.
From this knowledge we can create a general rule:
If any one number occurs twice or three times in just one unit then we can remove that number from the intersection of another unit.
This said, there are then four types of intersection:
A Pair or Triple in a box
- if they are aligned on a row, n can be removed from the rest of the row.
A Pair or Triple in a box
- if they are aligned on a column, n can be removed from the rest of the column.
A Pair or Triple on a row
- if they are all in the same box, n can be removed from the rest of the box.
A Pair or Triple on a column
- if they are all in the same box, n can be removed from the rest of the box. |
|
There are a whopping 20 candidates to be removed here – using seven Pairs and three Triples. Can you spot them all? Answers on page X. |
| |
| |
| |
| |
| |
| |
| |